Recursion Basics: Base Case and Recursive Call
Disclaimer: This material was taught in the JavaScript Algorithms and Data Structures Masterclass on Udemy by Colt Steele, which I highly recommend.
This article will go over the base case and recursive call and identify them in a couple of recursive functions. Recursion is a method of solving a problem where the function calls itself again and again — and, on each call, breaks its initial input down into smaller and smaller pieces.
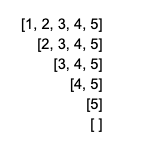
Let’s say a function is called with an array such as [1, 2, 3, 4, 5] as its initial input. In using recursion, the first time the function is called, it will run its operation with the first element, 1, as the function will then again be called on the smaller piece: [2, 3, 4, 5]. In receiving [2, 3, 4, 5], the second function call will run its operation using the second element, 2, before the function will again be called on the smaller piece: [3, 4, 5]. And on and on, until the array is empty [].
A recursive function is made of two components:
1) Base case: the condition when the recursion ends and the function ceases to call itself again. Because a recursive function calls itself, it is easy to write a function incorrectly that ends up in an infinite loop. Without a base case to end the recursion, the function will run forever (or until the program crashes/is stopped).
2) Recursive call. The recursive case is when the function calls itself — over and over again with a smaller portion of the initial input.
Okay, so what does a recursive function look like and how do we identify the base case and recursive call? Let’s take something simple such as a factorial function, which takes a given integer and multiplies that number with all of the integers below it (factorial of 3 returns 3 * 2 * 1 = 6). Below is an example, in JavaScript, of factorial without the use of recursion.

Now, let’s look at factorial with recursion, and identify the base case and the recursive call:
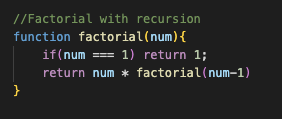
Recursive call: return num * factorial(num - 1). On each recursive call, the total product will be multiplied by the number (num), while factorial will be called again with that number minus 1.
Base case: if(num===1) return 1. The function will run until the number equals 1, at which point we will take the total product and multiply it by 1.
For another example of the base case and recursive call, let’s look at a function that takes in an array and returns its product (i.e. [3, 2, 4, 1] //=> 24):
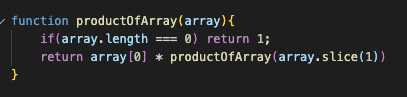
Recursive call: return array[0] * productOfArray(array.slice(1)). On each recursive call, the total product will be multiplied by array[0], while productOfArray will be called again with array.slice(1) — what remains of the array after removing the first element of the array.
Base case: if(array.length === 0) return 1. The function will run until the array is empty, at which point we will take the total product and multiply it by 1.
For one last example, let’s look at a recursive version of the function power that takes a number (base) along with how many times that base will multiply by itself (exponent). power(base: 5, exponent: 3) = 5³ = 5 * 5 * 5 = 125:

Recursive call: return base * power(base, exponent - 1). On each recursive call, the total product will be multiplied by the base, while power will be called again with the same base, but with its exponent subtracted by 1.
Base case: if(exponent === 0) return 1. The function will run until the exponent is 0, at which point we will take the total product and multiply it by 1 — any number to the zero power equals 1 (n ^ 0 = 1).
Often the issue with the recursive call is identifying what goes in the new, smaller input for the next call of the function. For integers and exponents (such as factorial and power), you may simply subtract or add from that number until you reach the base case. For arrays (such as productOfArrays) use slice, the spread operator, or concat to make copies of the initial arrays (that are, in virtually all cases of recursive calls, smaller than the initial array until you reach the base case of an empty array: []). If you have a string, you can use methods like slice, substr, or substring to make copies of strings. If you have an object, you can make copies with Object.assign or the spread operator.
